-
Rise of the Arrays
It’s been a little while since I blogged about analyzing radio signals so I thought I’d write a bit more about what I’ve been up to.
Behold: stamps!
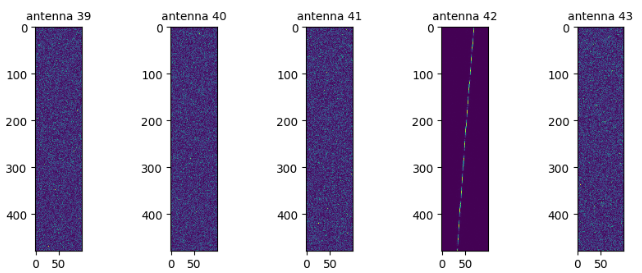
Stamps?
A stamp is the casual name for the input data from a radio telescope array, with a separate reading for each antenna, in a small range of frequencies, where a first pass on the data saw “something interesting”. This data is stored as complex voltages, because it’s basically a voltage going through a wire in a sensor, but you can graph its magnitude as yellow = strong signal, blue = weak signal, and that’s what I’m showing here.
This data is from the MeerKAT telescope in South Africa. Right now, the way this system works is roughly that every five minutes, the telescope records 60TB or so of data. We do a pass over the data to look for interesting stuff, and then when we find interesting stuff, we save a little neighborhood of relevant data in the “stamp”.
What is a Radio Telescope Array?
When I say “radio telescope”, think a big dish that looks like a satellite dish but it’s like 40 or 300 feet across. Not the sort of telescope you look into with your eyes. When I say “radio telescope array” think a whole bunch of these big dishes in a flat desert in the middle of nowhere.
Why Radio Telescope Arrays?
You can see that in this data, antenna 42 is showing “something”, and the other antennas are showing “nothing”. Unfortunately, that means this is not aliens. An alien signal would be coming from very far away, so it should show up pretty similarly in all the different antennas.
This is useful data to have, though! “Traditionally”, i.e. in most radio telescope searches for aliens in the years 1990-2020, the best method for distinguishing alien signals from other stuff has been to look at the shapes on these charts.
-
Big blob: a wide-band radio signal, could be a pulsar, quasar, interference
-
Vertical line: an artificial signal moving in unison with the receiver, i.e. on Earth, so it’s interference not a signal
-
Diagonal line: maybe an alien!
The biggest problem with these searches is that diagonal line does not necessarily mean alien. It just means a radio signal from a source that is not sitting still on the surface of the earth. We have tried to get around this by doing a “cadence analysis”, i.e. moving the telescope to point in different directions, and seeing if that makes the signal go away. This doesn’t get rid of everything, though, because sometimes a signal will just appear and disappear because it’s faint.
The array is cool because now we have a new, very powerful way to analyze signals - we can compare how the different antennas recorded the same event.
Wow?
Back in the 70’s, the Wow signal got people excited that maybe we were sensing an alien signal. That signal was about 30 times stronger than baseline noise. But, nowadays we pick up signals that strong all the time. Just turn on your radio telescope, wait five minutes, and you’ll probably see a couple of them. The sample signal I pasted above is about that strong.
Yeah, there’s a lot more radio interference out there nowadays. Still, it seems pretty clear to me that the Wow signal was some sort of radio interference. We didn’t have any strategies at all, back then, for differentiating narrow band interference from real alien signals. Academia isn’t really set up to clearly communicate information like, “In the past fifty years, it’s become slowly obvious to most practitioners that Theory X is incorrect.” If it was set up that way, though, I think the general consensus nowadays would be that the Wow signal was just terrestrial interference.
Complex Numbers
Radio telescope arrays are not just redundant copies pointing at the same thing. They also have very precise timing measurements. It’s precise enough that you can tell when a radio signal arrives at one antenna slightly before arriving at the other antenna. You can use this to very precisely determine of the precision of an astronomical radio source, like a pulsar.
Not only do you have two real numbers that are supposed to be very close to each other for a real signal, you have two complex numbers that are supposed to be very close to each other for a real signal.
This lets us, in theory, differentiate between a signal that is coming from a local source like an airplane or a satellite or a cell phone, versus a signal that is coming from extremely far away, like an alien planet.
Now What?
Well, our system is operational on MeerKAT and recording stamps. We now have far too many stamps to analyze them with our current set of tools. So we’ll need some better tools….
-
-
Notes on Inductive Programming
After the overwhelming popularity of last week’s blog post taking notes on an AI paper, I thought I’d continue the series.
So there was a reference in the Chollet paper to the paper Inductive Programming Meets the Real World, which sounded interesting. Let’s check that out today.
Background
But first, what is inductive programming? Let’s check Wikipedia.
Jeez. There’s dozens and dozens of references, all this history. I consider myself reasonably knowledgeable about general computer science things, and yet I have never heard of inductive programming. It gives me a sensation of… vertigo? Like you peer over the edge and see instead of a little ridge, the hole goes deep, so deep you have to give up hope of ever truly exploring its boundary.
But basically, it’s learning programs given some sort of incomplete specification. As opposed to, learning programs given an entirely complete specification, which is “deductive” programming. Naturally I haven’t heard of that at all either.
How do these people get Wikipedia pages? Is this good for anything? Does it actually work? I guess this is just the divergence of academic and industrial computer science.
I guess the most logical sort of incomplete specification is, here’s a bunch of inputs and outputs. That makes sense. Any other sort of formalistic way to specify anything seems like a pain.
Meeting the Real World
The paper has a couple Microsoft authors and seems to allude heavily to this one feature in Excel where it will autogenerate transformations for columns. It’s funny that they don’t explicitly say anything about it, but I’m guessing there’s some half-research half-product group, and they built this feature for Excel and also published this paper about their work.
They say that originally inductive programming dealt with simple, abstract logical tasks like sorting or reversing a list. There’s no citation here, though. Huh! How exactly do you learn to sort a list from examples? That doesn’t seem simple at all to me. I mean, deep learning generally cannot do it. What form of sort does it learn? Insertion sort?
The authors also seem to care a lot about “no code” operation. Helping people out who don’t know how to program. That’s all well and good, but it seems like academic research is precisely the opposite way to investigate no-code tools. Academic research is good if you are like, trying to solve abstract math puzzles, or decoding radio telescope signals, something where there’s no possible profit, so the best funding is going to be through the academic channel. Whereas the top ten no-code tools out there are all going to raise more money than any academic group has access to.
Recent Techniques
This section is like a little survey covering different techniques for inductive programming. My point of view is, I feel like there is a “general skill” for programming, and I am curious about which of the different techniques seem to me like promising ones for obtaining this general skill.
DSL synthesizers
To me, the whole idea of a DSL is like, a way of stretching your techniques to go a little bit further, but something that fundamentally doesn’t scale very far. It’s like the Jekyll markup language. (On my mind since I was just debugging some Twitter card markup problems with this blog.) It’s great for building websites, but if you try to make everything obey this restricted form of
strip_html | replace foo bar | remove_newlinesyou’re eventually going to create a confusing mess.In particular, is there some DSL synthesizer that could learn to sort lists, if it hadn’t seen this before? It seems like cheating to put something like “insert into a sorted list” into the DSL. So you’d have to get down to basic enough things like appending to a list, comparing… at that point it isn’t really a DSL any more.
Meta-synthesis frameworks
This is just more DSL. Ways to handle even larger piles of DSL rules. Again I don’t see how it could learn to sort lists.
Higher-order functions
This sounds cool but I don’t really understand how it works. In the example they invent an auxiliary function which, when applied to a
fold, reverses a list. That… makes sense. How does it work though? Can it do sorting? I can’t tell, here. I might have to dig in more, hunt down this Henderson paper.Let me think about it for a bit. How would you automatically program a list-reverser? You could guess that the first step would be popping a list apart into head and tail. But then what? Maybe what you really need is to work backwards, to guess that you need to calculate two things, you need to calculate the last item of a list, and you also need to calculate the reversed everything-but-the-last. That doesn’t seem like it’s making progress, though. Well, I don’t know how this could work. But allegedly Henderson does. Seems like a promising lead.
Meta-interpretive learning
This section annoys me because it’s like, okay first let’s think of everything in terms of Prolog. And then the good news is, hey we have reduced search times for some task. It’s like looking through a portal into an alternate universe where Prolog matters, everyone knows that there is important work done in the world by Prolog, and improving the performance of Prolog programs is obviously an interesting idea.
I tried and failed to dig through the Prologisms here. I am dubious that difficult goals will look like proving
boss(lucas, lucy).New kinds of brute-force search
Now this sounds promising! It doesn’t really get into the details, though. Just says that there are so many possible programs, it’s hard to check them all, and has some references. Okay.
Conclusion
New approaches are needed which allow users to decompose more complex tasks into sufficiently small subtasks and then incrementally compose the solutions.
Yes… although really once you can correctly decompose a programming problem into subtasks, you’ve often done the hardest part. So perhaps this isn’t really a no-code thing to do, but just a problem for the automatic code writer.
List reversing is a good example here. The simplest program to reverse a list adds in some “auxiliary data”. In pseudocode:
def reverse_and_add(x, y): "Does reverse(x) + y" if empty(x): return y return reverse_and_add(tail(x), cons(head(x), y))Once you know you’re implementing
reverse_and_add, it’s a lot easier than when you’re just told you have to implementreverse. And thenreverseis a special case.At some point this was a “trick” I was learning. These recursive programs, often you want to tack in some extra information to come along on the recursive structure. You need to be “building the answer” as you go along. Like when you have a data structure and only later do you think, ah gee it would be nice if every internal node in this tree also kept track of the total weight of its subtree.
How would a computer get here? I don’t know.
Well, this was interesting, sort of a mini-survey. I like writing down these notes - honestly I just take far more detailed notes than I do when I’m not going to make them public, and I think about these papers a lot more, and that’s the best part about writing these posts.
-
Notes on 'On the Measure of Intelligence'
Recently I’ve been interested in François Chollet’s thinking on generality in artificial intelligence. Even more recently I’ve been reading this paper, On the Measure of Intelligence. I thought I’d blog some notes to sort of encourage myself to think more intelligently about it.
I’ll just awkwardly munge together my opinions and Chollet’s opinions in these notes. Go read his paper if something here intrigues you and you want to learn more.
What is “intelligence”?
Chollet thinks that most AI progress has been on “specific tasks” and to be really “intelligent” a system needs to be able to handle general tasks. AI has been successful at specific tasks, like playing chess, or recognizing handwritten digits. Arguably this is not “intelligence” because you aren’t testing the system’s ability to generalize, you aren’t testings its “ability to handle situations it hasn’t seen before”.
Even the Turing test is not really general enough in this view. The Turing test is a weird bar - personally I feel like I am administering a Turing test to new chat bots when I test out something like character.ai. But it’s like a software engineering interview. Just because I believe I can tell when something isn’t intelligent doesn’t mean that I think a program that fools other people is important to try for.
Chollet talks a lot about, what counts as generalization. This seems like a spectrum to me, there’s no clear line where more generalization is a lot better, generalizing does seem like a good feature for a system to have, okay.
IQ tests don’t seem all that great for measuring AI systems. It’s just too much of a diversion to go do the things that make you better at IQ tests. Or at least, why bother testing on the same exact thing that humans test on? There’s a PR sense where it convinces the public that AI is happening, but it doesn’t necessarily lead in the right direction.
Some interesting criticisms of games
OpenAI trained the AI “Five” to play Dota 2. At first it beat human players, but a few days later after the humans practiced they could beat it. It’s essentially a very slow learner by human standards if you measure by “gameplay time” rather than “clock time” - the AI needed 45,000 years of gametime, and even if in practice you can do that fast on a big cluster, it’s still showing that the underlying learning algorithm isn’t working as well as whatever humans do, because Dota pros spend more like a single digit number of years, max, learning Dota.
AlphaGo and AlphaZero haven’t been useful outside of board games. This is sort of true, but on the other hand IMO they provide a good demonstration of how you can build a larger system out of smaller parts, with different parts using different AI models. And this is basically how we are making progress on self-driving cars, or maybe the fact that self-driving cars are working slower than expected is an indicator that things aren’t working well enough here.
The AI systems can learn on hundreds of Atari games but still don’t play a new Atari game very well. A human expert game player, on the other hand, is usually pretty good on their first playthrough of a new game.
It’s interesting to think about chess historically… there were people described in this paper who assumed that solving chess would naturally require a huge array of mental skills since those are what people used. Of course in practice the alpha-beta algorithm is super useful for chess and not really useful for anything that isn’t like chess. Back in the 90’s when I was taking undergrad AI classes it did seem like people thought the chess and game work would be more relevant than it’s turned out to be.
Athleticism
I never thought of this before, but a parallel question to “what is intelligence” is “what is physical fitness”.
Obviously there is such a thing as physical fitness. You just know Lebron James is going to be better at juggling than me if we both practice for a day.
But if you think of physical fitness as “performance on an average task” then you could easily come up with an incompatible metric. What if you took an average position, anywhere in the solar system? You’d end up thinking that humans all had fitness zero because we couldn’t do anything in outer space. Lol.
Robots certainly don’t have general fitness if you think of it in a human sense. Even these industrial robots tend to be like, this robot installs the rear windows on a Mazda CX-9, and it does it way faster and more accurately than a human can. But it can’t juggle even as well as me, with days of practice. Much less as well as Lebron James can juggle.
Dimensionality
Humans have some parts of intelligence hardcoded. Like dimensions. Humans have all this instinct for solving 2D geometry problems, and 3D geometry problems, and then you give the simplest of 4D problems and it’s just completely impossible.
Another funny example is shortest-path problems. Humans are pretty good at instinctively finding the shortest path that meets some conditions. But they are terrible at finding the longest path. For a computer it’s basically the same thing!
Chollet thinks it’s important to give an AI system a very similar set of priors to the set that humans have. I am not sure if I agree with this or not. Things like object persistence, small number manipulation. I dunno - personally I feel like the whole notion of “prior” is overrated because it’s mathematically convenient. I don’t really think the human mind works with priors. A prior is more like, an awkward way of badly summarizing someone’s belief system, hinting at some deep mathematical optimization system that isn’t really optimal in practice.
“Skill-acquisition efficiency”
Chollet’s definition of intelligence:
The intelligence of a system is a measure of its skill-acquisition efficiency over a scope of tasks, with respect to priors, experience, and generalization difficulty.
Personally, I neither agree nor disagree with this statement. It just doesn’t really bother me how we define intelligence. I guess that makes it funny that I am thinking so much about this paper that is entirely about defining intelligence!
What definitely seems true is that current AI systems require too much training data. Humans learn things with a lot less training data, and we don’t really have incredible priors that are solving the problem for us. The best example I think is multiple video games. You play 100 Steam first-person shooters, you’re going to pick up the 101st pretty quickly. Like you play it through once and you do pretty well on that playthrough.
There is not quite an analog for, study this small number of entities and learn what you can. Like meditating on it. How much can you train on a single image? The whole supervised learning thing doesn’t really make sense on it. You need some other… some other something.
Personal aside
I am pretty interested in video games and AI playing video games. I tried for a while to make a reinforcement learning agent play Slay The Spire. I fell completely short, mostly because it seemed like I would never get enough training data to make any of the RL techniques work.
What it “feels” like is that the AI doesn’t really understand things that a human picks up very quickly. Just the basic mechanics like, okay we have a deck of cards, every turn we are drawing five cards from that deck. An AI model isn’t learning that underlying logical structure. Deep learning can learn this but in some crazily inefficient way where it’s memorizing a ton of pairs of inputs and outputs. All that inefficiency I think just adds up to not letting you play the whole game.
Why is this interesting at all? I don’t know, maybe it’s like a curse. I have this instinct where I try to do something for a while, and then I end up thinking, hmm, I wonder if a computer could do this better. And then I think the same way when I’m doing, not some professional mundane task, but having fun, playing a game. I end up a bit bored when a computer can solve a game - like chess - but I think the games that computers currently can’t solve - like Magic: the Gathering or Slay the Spire - are pretty interesting. But if an AI did solve them, I think I would get bored by them. I guess that’s okay though.
Evaluating general intelligence
Okay, so there’s a whole lot of notation on how to evaluate intelligent agents. Basically it’s like, instead of having one task, you have a bunch of task-categories and what you really want is to pick up each new task-category quickly.
I am not sure what exactly the difference is between this and a more normal model. You can just think of a task as a more general thing. Like instead of “is this picture a cat or a dog” your task is “your new task: categorize cats and dogs. here’s n examples, categorize example n+1”. Yeah, you can add up the scores different and look at asymptotes of things, but I feel like it all adds up to just saying, we need to be measuring more abstract, more general tasks. And then you can have thetas with lots of subscripts, but, I just know that’s not quite going to stick in my head.
Algorithmic complexity
The Algorithmic Complexity of a string is the length of the shortest description of the string in a fixed universal language.
Like a Turing machine. Although in practice Turing machines are quite inconvenient, I’d rather go with some minimalist lisp here.
So literally should we just be looking for small Lisp programs that generate given outputs? I mean, that seems like a possible thing to try to code. The best ARC solution on Kaggle, as far as I can tell, is brute forcing combinations of some hard coded set of 100 or so functions.
There’s some point here that I don’t understand. Chollet doesn’t want to simply measure the goodness of a solution by how short it is. Instead, first there is a definition of “generalization difficulty”. But, the generalization difficulty refers to the shortest possible of all solutions that achieve at least a certain skill rate during evaluation. This seems… completely uncalculateable? If you could actually find the shortest program that generates a particular output that would probably violate some sort of diagonalization principle. I’m not sure whether I’m understanding this right, but if I am understanding it, then I don’t think I agree with it.
I like the more basic point of, just looking for small programs that generate a particular output is a very general task by its nature. If anything, the 2D grids of ARC are anthropocentric. A 2D grid isn’t all that natural. It’s just a really great fit for human eyeballs, terminal programs, and GPUs. A plain old list is more logical; you use lists all the time in your head like, I have this list of three errands to do before dinnertime. I’m never making a 2D grid in my head to go about everyday life.
Program synthesis
“Program synthesis” sounds pretty cool. Chollet says his line of reasoning “encourages interest in program synthesis”. Cool.
I wonder what the simplest program synthesis task is. ARC is pretty simple but you can see from the top scoring results that you get a ton of value by hardcoding in 2D-specific transforms.
I know deep learning has trouble on just basic O(n) recursive problems like reversing a list or adding two numbers. The whole structure of deep learning doesn’t really set itself up to learn a pattern of doing one particular thing a number of times recursively. The gradients disappear, or by the “lottery ticket” hypothesis you just don’t have enough lottery tickets to make the whole system work in one click. You need some way to learn substructure without having the whole problem solved.
ARC
Oh, maybe this paper was written slightly before the ARC dataset was released? I guess I am thinking this whole thing through backwards. Ah well.
So Chollet has all these priors, these assumptions that he thinks are good ones for ARC.
- Object cohesion
- Object persistence
- Object influence via contact
- Shape upscaling or downscaling
- Drawing lines, connecting points, orthogonal projections
To me this is aethetically displeasing. Objects that influence each other by touching each other. Okay, the visual real world works that way, but 2D arrays generally don’t. But fine. It just makes me think that for ARC you want some logical core and then you want to boost it up by giving it some sort of hard coded 2D-grid-handling stuff.
There’s some interesting reading linked on program synthesis, I’ll have to check that out.
From working on radio telescope stuff recently I am starting to develop this theory, that GPU programming is going to overwhelm CPU programming in every scientific or numerical field, and the whole AI / deep learning boom is just a leading indicator of this, it’s happening there first because there’s a huge industry investment into Tensorflow and PyTorch and so on, but it’ll happen in other places soon. It’s way too hard to program CUDA stuff for most academic research groups to do it well. So maybe there’s something promising here.
More on program shortness
Chollet writes about a possible ARC approach.
Select top candidates among these programs based on a criterion such as program simplicity or program likelihood. Note that we do not expect that merely selecting the simplest possible program that works on training pairs will generalize well to test pairs.
That’s a little weird to me. Why would the shortest possible program not be the best way to describe something?
Eh, I’m probably getting too hung up on this. There might be some sort of “cheater programs” which are doing something like, hardcoding some exceptions, hardcoding in part of the output, and if your training data is really small like three examples, this cheating might end up being shorter. So you would just have a difference between “is your program aesthetically cheating” versus “is your program super short”. Seems like the sort of thing you can only really know in practice.
In practice, it seems like the biggest problem by far that we can’t actually find the shortest program that maps inputs to outputs. I’m not entirely sure about that but that’s my take from reading the top ARC solution writeup.
Conclusion
I’m interested to read more about program synthesis. I have a vague feeling that you should be able to do better with clever GPU stuff, and also by doing some simultaneous forward and backward searching where you look for overlap. (That’s how rewrite search in Lean to simplify a given mathematical expressions into a target works, for example. And in general automatic theorem proving often is more successful working backwards than forwards.)
But I don’t think that will quite be enough, you need some way to learn interesting things even when in “solution space” you are nowhere near the right answer. Hmm.
-
Embracing My Inner Blub Programmer
I always feel a little bit guilty about Lisp. I am supposed to appreciate Lisp. It’s a fine wine and as a member of respectable society I should hold it in high esteem. But, I’m not quite there. I’m not opposed to Lisp, per se, I just never end up using it for very much.
This week is no exception. I am not writing any Lisp this week. Quite the opposite - for the first time in a while, I am writing big chunks of C++.
The Bad
It’s very obvious when you write C++ after using languages like Python or JavaScript for a while that C++ has problems. Ancient problems that I remember Java fixing back in the 90’s. The problems with C++ are so glaring, I run into programmers who are surprised that such things are even possible.
-
When you write a new class you have to split logic into
.hand.cppfiles, half repeating yourself. -
If you accidentally access of the end of an array, your program will simply crash with no error message reported.
-
If you forget to initialize a member variable, your program will often set those variables to zero, but sometimes it will just fill them with quasi random data.
-
You either have to manually free memory that you allocate, or use solutions like
unique_ptrthat are more complicated than any reasonable language offers.
The Not So Bad
At least C++ is getting better. The last time I wrote a lot of C++ was working for Google, 2005-2009, and I don’t think we had even fully adopted C++98. So I’m still a decade behind the times, learning the various C++11 things.
unique_ptrandshared_ptrare good; they let you mostly avoid remembering to delete your own pointers.mutexandcondition_variableare good as well. And in general with GitHub,cmakeandmesonthere are a decent amount of libraries out there that do common things. Not like Python or JavaScript where you have solutions for everything, but it’s a lot better than nothing.The Actually Good
So why C++ at all? Well, this is my favorite API of the week:
cublasCgemm3mStridedBatched(cublasHandle_t handle, cublasOperation_t transA, cublasOperation_t transB, int M, int N, int K, const T* alpha, const T* A, int ldA, int strideA, const T* B, int ldB, int strideB, const T* beta, T* C, int ldC, int strideC, int batchCount)It’s a shortcut to run code equivalent to these nested loops, on a GPU…
for (int p = 0; p < batchCount; ++p) { for (int m = 0; m < M; ++m) { for (int n = 0; n < N; ++n) { T c_mnp = 0; for (int k = 0; k < K, ++k) c_mnp += A[m + k*ldA + p*strideA] * B[k + n*ldB + p*strideB]; C[m + n*ldC + p*strideC] = (*alpha)*c_mnp + (*beta)*C[m + n*ldC + p*strideC]; } } }…but you can also conjugate-transpose
Abefore running this matrix operation. I was pretty excited, I literally wanted a matrix to be conjugated and transposed, and I thought this was the sort of abstract mathematical fun that I had given up long ago with the transition to computer science.See this Nvidia blog post if you’re curious for more detail, but basically this code is multiplying sequences of matrices that you’ve stored in some regular way in memory.
Blub
I feel like this is why I always end up developing in Blub nowadays. I’m never choosing programming languages based on the most powerful generalist language. I always have some narrow task - from GPU matrix operations to making a responsive website where you can drag stuff around - and having a library that’s well suited to the task ends up being more important to me than having macros.
It’s not the same but at least I sort of get to use Lisp macros while developing in Emacs. I’ll take another look at VS Code once they implement
C-x-(,C-x-), andC-x-e. -
-
H1 Review
About six months ago I made some New Year’s resolutions, and I thought I might write a Q1 update, but here we are six months later and I haven’t written anything about how it’s going. So… it’s an H1 update.
1. Calorie Counting
Man this one is going well. This is the most effective diet I’ve ever been on, and I’ve been sticking on it for six months. It’s pretty simple to describe - I just count calories, using the default iOS health app. I am actually below the official government “not overweight” line for the first time in my adult lifetime.
So, yeah, great, I just need to keep it up.
It’s somewhat less simple in practice than it is in theory. It’s really not straightforward to figure out how many calories are in a given food. Even the best information on the internet will not be accurate to within about 20%. The “counting” isn’t the hard part, it’s the “estimating calories for a given food item” that is the source of errors.
I also just haven’t been drinking very much. Two days this past six months.
2. Astronomy Publication
I don’t think this goal is on track. Six months ago I thought it was plausible for my work on processing the Green Bank data to get rolled up into some summary paper, soon, describing our work on SETI search there. But, it’s looking like there isn’t a critical mass of people who want to work towards publishing a big analysis of Green Bank data this year.
I’m shifting the strategy here a bit. I’m focusing on this new repository of SETI-search and general radio astronomy algorithms, with two main principles.
- Faster than any alternative, via writing in C++ and CUDA
- Full support for interferometer arrays
My goal is to get this new software adopted as the production SETI search library for both MeerKAT and the VLA by the end of the year. These are interferometers rather than big single dishes, these are the new hotness, I should really write some separate blog post on just “what are interferometers”.
I’m less focused on “what algorithm exactly is it running”. I have a lot of ideas for algorithmic improvements, but everyone has a lot of ideas for algorithmic improvements. There are dozens of cooks in this kitchen. The limiting factor is the ability to implement search algorithms, and to implement them efficiently enough to actually run them on the scale of terabytes-per-minute.
So, if there arises a consensus in the scientific community that algorithm X would be a fantastic way to analyze incoming radio telescope data, I’d be interested in writing an efficient implementation of X, and integrating that into seticore.
I’m also less focused on “publication”. That’ll come in time and I don’t really want to work on a publication just for the sake of getting a publication - there’s too much of that in academic-world already.
3. Exercise
I’ve just been cranking along here. Working out four times a week is a pretty regular part of my routine now.
It’s funny, I don’t really think exercising has helped me lose weight. It just doesn’t seem like it correlates. But the reverse is definitely true - losing weight helps me exercise better. I have somewhat more endurance, and way more ability to do pullups.
I do think that exercising gives you more energy through the next day. Same with not drinking. My energy level the next morning is really boosted when I exercise and when I don’t drink.
4. Blogging
I’m a little behind on this one. Just a couple weeks behind, though. I wrote a script to compare how I’m doing.
I used to blog and try hard to get people to read it. I just don’t have the mental energy to do that every week. And it’s a totally different blog post. The stuff people want to read is like, zingers about Uber when Uber has been in the news. Thumbnails of GPT-3 which are easy to exaggerate.
The stuff I want to write is like, I read some books about the history of Mexico, now I have all this information swimming in my brain, and I feel like I should do something with it. I need to get it out, need to stop just thinking random uncorrelated thoughts on the topic and see if I can boil down what I really think. I want to reflect on the Drake Equation or AIs playing board games or the importance of slug welfare.
So, I am just not going to try to get people to read this. Not now, at least. But I’m going to keep writing. I’ll try to catch back up - I fell behind when I caught Covid a couple weeks ago.
Looking Forward
I’m feeling pretty good about the whole resolution thing. Calorie-counting has been a great success, astronomy publication has not been a success but on a meta-level I feel like the explicit goal-setting process was useful there because it made me think a bit harder about what to focus on.
It’s funny because at Google and Facebook I really hated the performance review cycle. One of the worst parts of working for a big company. But I like the process of having goals and being tough on yourself for not hitting them. I just hated being reminded that I was in a system where some other person’s opinion of my performance was really important to me. Every single time it would make me think, I wish I wasn’t working here. I should quit. I should be testing myself against what I can achieve in the world, not against what some coworker thinks.
Onward to H2. I’ll aim to do a similar writeup at the end of the year.